Autonomous cars, pedestrians, and the game of chicken

I was interested to read this article in The Conversation last month by Jason Thompson (University of Melbourne) and Gemma Read (University of the Sunshine Coast), about the interactions of humans and autonomous cars. In particular, they use some very simple game theory to represent the interaction between cars (autonomous or otherwise) and humans:

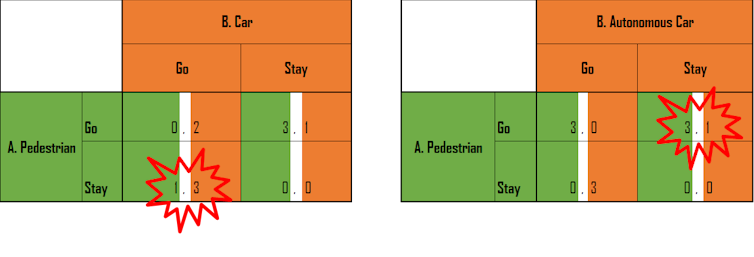
A simple example of how this might happen comes from game theory. Take two scenarios at an intersection where pedestrians and vehicles negotiate priority to cross first. Each receives known “pay-offs” for behaviour in the context of the other’s action. The higher the comparative pay-off for either party, the more likely the action.

In the left-hand scenario below, the Nash equilibrium (the optimum combined action of both parties) exists in the lower left quadrant where the pedestrian has a small incentive to “stay” to avoid being injured by the manually driven car, and the driver has a strong incentive to “go”.

However, in the scenario on the right, the autonomous vehicles has a desire to act flawlessly and pose no threat to the pedestrian at all. While this might be great for safety, the pedestrian can now adopt a strategy of “go” at all times, forcing the AV to stay put.

Here's their associated diagram. The red explosions show the Nash equilibrium in each case:

However, I think they have their analysis wrong. I don't think they've really considered the game theory implications here fully. In the game on the left, the car has a dominant strategy to "Go" - going provides a payoff that is always higher than staying. The car driver should never choose to stay, including if the pedestrian chooses to "Go" as well. But, if both pedestrian and driver choose to "Go", then the car runs over the pedestrian. It's hard to see how the car driver is better off going if the pedestrian goes (unless the disutility of washing the blood off their car really is less than the utility gained from getting through the intersection faster).

Similarly, in the game on the right, the pedestrian has a dominant strategy to "Go". But again, would they really choose to "Go" if the car is going too? Maybe in Thompson and Read's world, pedestrians aren't seriously injured or killed when they run into cars, but in the real world it seems like a pedestrian would be pretty stupid to go if a car is going.

A more realistic representation of the game is in the payoff table below. If both the car and the pedestrian go, then both lose. The loss to the car driver is pretty high (damage to their car; maybe jail time for running down a pedestrian), but not as high as the loss to the pedestrian (being injured or killed by a car is pretty serious). If car or pedestrian goes, and the other doesn't, then whichever one goes gets a larger positive payoff. If both car and pedestrian stay, then a standoff ensues, and both get a payoff of zero.

Where is the Nash equilibrium in this game? We can use the 'best response method' to find the equilibrium. To do this, we track: for each player, for each strategy, what is the best response of the other player. Where both players are selecting a best response, they are doing the best they can, given the choice of the other player (this is the textbook definition of Nash equilibrium). In this game, the best responses are:

1. If the car chooses to go, the pedestrian's best response is to stay (since 1 is a better payoff than -5) [we track the best responses with ticks, and not-best-responses with crosses; Note: I'm also tracking which payoffs I am comparing with numbers corresponding to the numbers in this list];
2. If the car chooses to stay, the pedestrian's best response is to go (since 3 is a better payoff than 0);
3. If the pedestrian chooses to go, the car's best response is to stay (since 1 is a better payoff than -3); and
4. If the pedestrian chooses to stay, the car's best response is to go (since 3 is a better payoff than 0).

There are two Nash equilibriums in this game: (1) where the car goes and the pedestrian stays; and (2) where the pedestrian goes and the car stays. Notice that both players in this game would be better off if they are the one to go, and worse off if they are the one to stay. But, if both choose to go, then they end up in the worst possible outcome! This is an example of the chicken game (which I have previously blogged about here).

A game with two Nash equilibriums doesn't really give us much guidance as to what the ultimate outcome will be. Both players want to go, but both want to avoid the situation where they are both trying to go at the same time. So, how do we solve this problem?

Currently, we solve the problem using a mixture of road rules and social norms. At pedestrian crossings, cars always stay and pedestrians can go. At traffic lights, cars and pedestrians stay or go depending on whether their light is red or green. At other places, pedestrians stay and cars go - that's why we learn as children to look both ways before crossing the road (a social norm).

However, autonomous cars create an interesting situation, as Thompson and Read highlight in their article. If autonomous cars are programmed to always give way to pedestrians (or, equivalently, to always avoid a collision with a pedestrian where possible), then that means the car will always stay. If the pedestrian knew (for sure) that the car was going to stay, they would choose to go. Every time. Suddenly, we end up in the top right box of the payoff table.

Why is this a problem? As Thompson and Read note:

Now imagine crossing a road or highway in a city saturated by autonomous cars where the threat of being run over disappears. You⁠ ⁠(⁠o⁠r⁠ ⁠a⁠n⁠y⁠ ⁠o⁠t⁠h⁠e⁠r⁠ ⁠mildly i⁠n⁠t⁠e⁠l⁠l⁠i⁠g⁠e⁠n⁠t⁠ ⁠a⁠n⁠i⁠m⁠a⁠l⁠)⁠ might quickly learn that ⁠⁠oncoming traffic poses no threat at all. Replicated thousands of times across a dense inner city, this could produce gridlock among safety-conscious autonomous vehicles, but virtual freedom of movement for humans – maybe even heralding a return to pedestrian rights of yesteryear.

Thompson and Read make the (obviously tongue-in-cheek) suggestion that a solution is for autonomous cars to occasionally, purposefully, run into pedestrians. That seems unlikely (though potentially effective).

Ultimately, this game of chicken is one that pedestrians are likely to win. So, while many are claiming that autonomous vehicles are the solution to traffic problems, they could actually end up making them worse.