The optimal queue

One of the biggest headaches that shoppers have to deal with is queues. Shoppers don't like having to wait, and if the queue is too long, some may simply give up without completing their purchase. But for store owners to reduce the length of queues (or eliminate them), they would face higher costs (at the least, they would need to hire more staff). So, eliminating queues is unlikely to be a good plan for stores. To see why, consider this recent article in The Conversation by Gary Mortimer (Queensland University of Technology) and Louise Grimmer (University of Tasmania):

Businesses face the challenge of identifying the optimum point where the costs of providing the service equal the costs of waiting. People in queues behave in ways that create direct and indirect costs for businesses. Sometimes customers will baulk and simply refuse to join the queue. Or they join the queue but renege, leaving because wait times are too long.

This behaviour leads to measurable costs. These costs are both direct, like abandoned carts, and indirect, like perceptions of poor service quality, increased dissatisfaction and low levels of customer loyalty.

There's lots of interesting points made in Mortimer and Grimmer's article (and for more on queueing, see my 2014 blog post on the topic). However, I want to highlight this diagram:

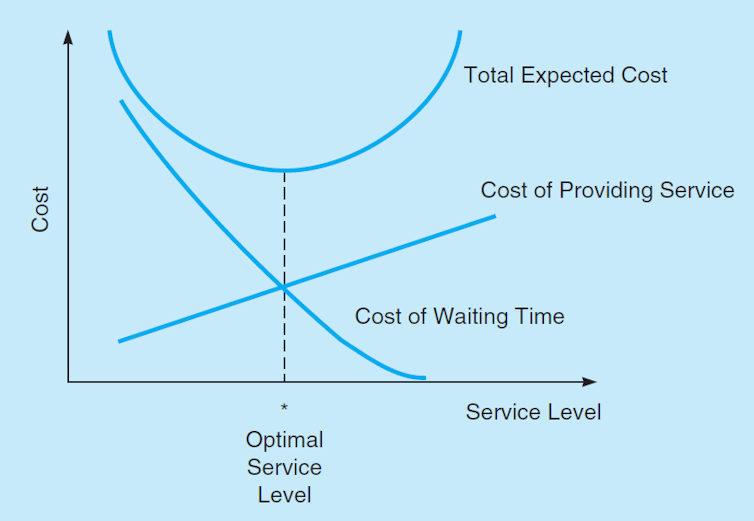
The diagram illustrates the optimal level of service. The y-axis shows costs to the store, and the x-axis shows the service level (where a higher service level is associated with shorter queues). The store is trying to minimise their total costs, but there are two marginal costs that they are trying to balance. The first cost is the marginal cost of providing service. This is upward sloping as we move from left to right, because each additional 'unit' of service level costs the store more than the last. To see why, consider your local supermarket. If it only had one checkout, adding another checkout would be fairly low-cost - the store would give up a little shelf space (which would entail an opportunity cost of some lost sales of items that would have been displayed there), and have to pay another worker to man the second checkout. A third checkout would entail more cost, as would a fourth, and so on.

So it is easy to see why the total cost of providing service increases, but why does the marginal cost (the cost of providing one additional checkout) increase? It's because each additional checkout is not as productive as the previous one. If you only have one or two checkouts in your supermarket, the workers on those checkouts are going to be going flat out all day. But if you add a seventeenth checkout, that checkout might stand idle during quiet periods (or days, or weeks), and that added cost is going to be spread over fewer customers, so the cost per customer for that checkout (the marginal cost of that checkout) is higher than the first ones. So, that's why the marginal cost of providing service is upward sloping. It is low when providing a low level of service, but increases as you provide higher levels of service.

The second cost is the marginal cost of waiting time. This cost increases when you provide lower levels of service, because the lower service levels, the more frustrated your customers will be. Perhaps they decide to leave the store without completing their purchase, or perhaps they complete their purchase but don't return in future. Either way, that is a cost for the store (an opportunity cost of foregone sales), and the cost is greater the lower the service level. An alternative way of thinking about this is that it is the marginal benefit of providing better service.

The optimal level of service is the level of service where the marginal benefit exactly meets the marginal cost (or, in this case, where the marginal cost of providing service is equal to the marginal cost of waiting time). That's the optimal service level, because if you moved in either direction, the cost to the store would be greater.

To see why, consider a point just to the left of the optimum on the diagram above. The store is offering a slightly lower level of service than optimal. It saves on the cost of providing a checkout, but that cost saving is less than the extra waiting cost it incurs (this is easy to see on the diagram - notice that the marginal waiting cost is above the marginal cost of providing service). That makes the store worse off.

Now consider a point just to the right of the optimum on the diagram above. The store is offering a slightly higher level of service than optimal. It encourages more customers to stay and purchase, saving on waiting cost, but that is less than the amount it saves on the cost of providing better service (again, this is easy to see on the diagram - notice that the marginal cost of providing service is above the marginal waiting cost). That also makes the store worse off.

The optimal service level is probably not to ensure that no customer ever queues. It is to keep the queues just long enough that it balances the marginal cost of providing better service against the marginal cost of lost custom.

Read more:

• Low price but high cost: The economics of queues